FCSC 2021 - Intro - guessy
It will probably take a lot of luck to guess the flag. Or some reverse engineering skills.
SHA256 (guessy) = f9388d92cbf5de8c92831555608162c672a99d164aed789638fcc91a66ab13e5.
Files :
Solving the challenge
First, let’s play around with the challenge binary. When we enter anything as input, we have Well it does not begin well for you. :
$ ./guessy
Give me the flag:
wow_such_flag
Well
But when our entry starts with `FCSC {` we have another message, and the binary asks us for a new entry:
```$ ./guessy
Give me the flag:
FCSC{
Ok so I see we have an understanding. Let's begin the difficult part now.
Now you can try to guess the next eight characters of the flag.
Well it seems that someone has trouble counting to eight.
General analysis
This binary is used to validate a flag entered as a parameter. There are 5 successive checks corresponding to the 5 parts of the following flag:
FCSC {aaaaaaaabbbbbbbbccccccccdddddddd}
We will analyze the functions that perform these checks in order.
Analysis of the main function
The main function is very basic, it just calls the validate function on the input read with fgets just before:
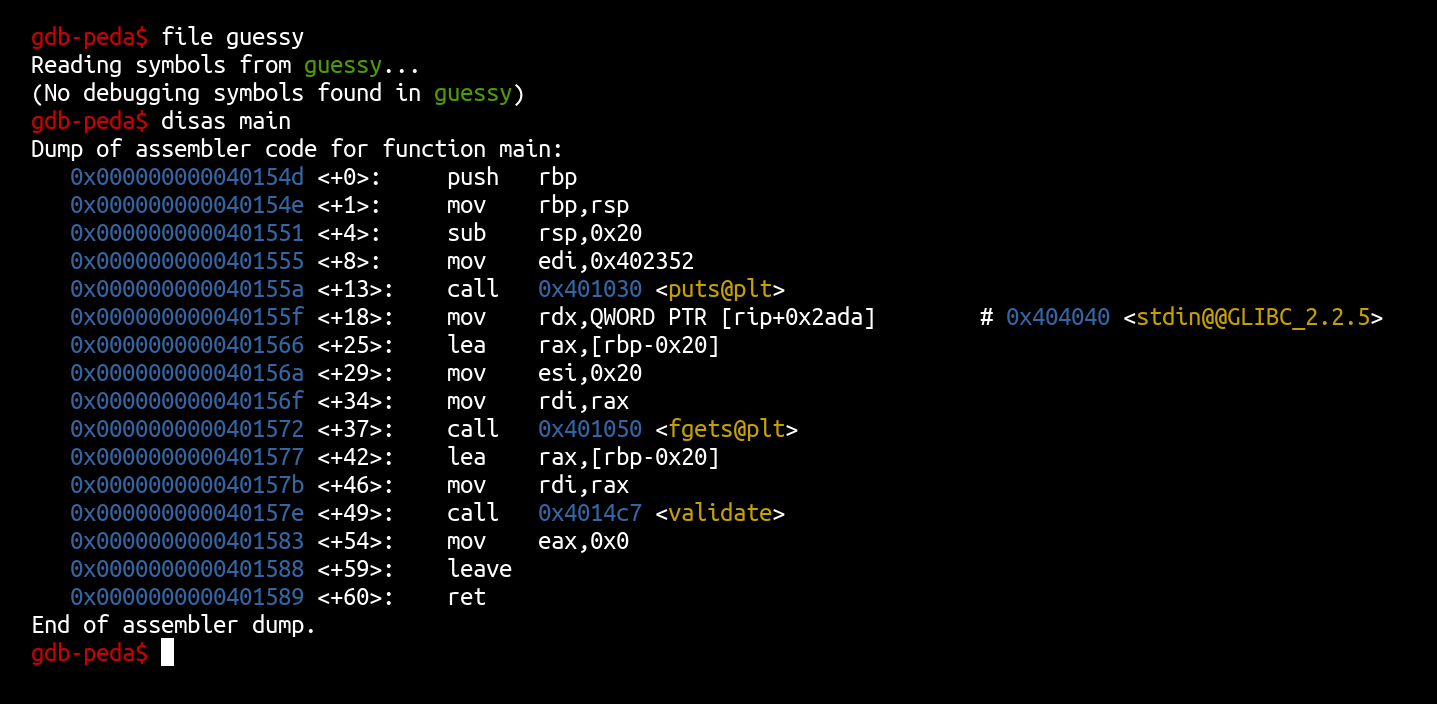
Now let’s disassemble the validate function.
Analysis of the validate function
The validate function checks the first 5 letters of the flag:
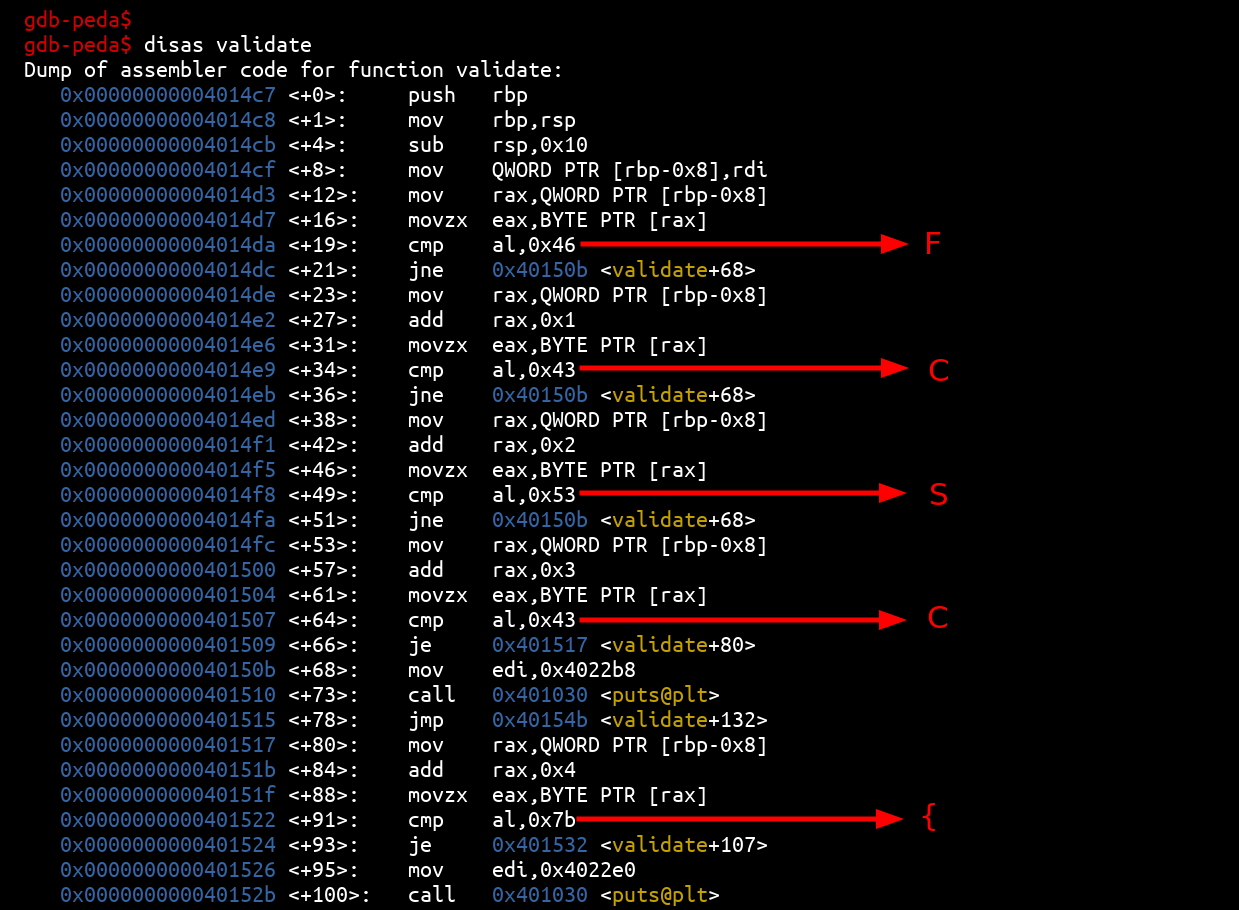
So we have :
FCSC{________________________________}
It then calls the difficult_part function for the rest of the checks.
Analysis of the difficult_part function
The difficult_part function contains 4 checks, each operating differently.
Part 1
The first check is a simple comparison of the flag letters in the order we entered with the expected ASCII values for those characters:
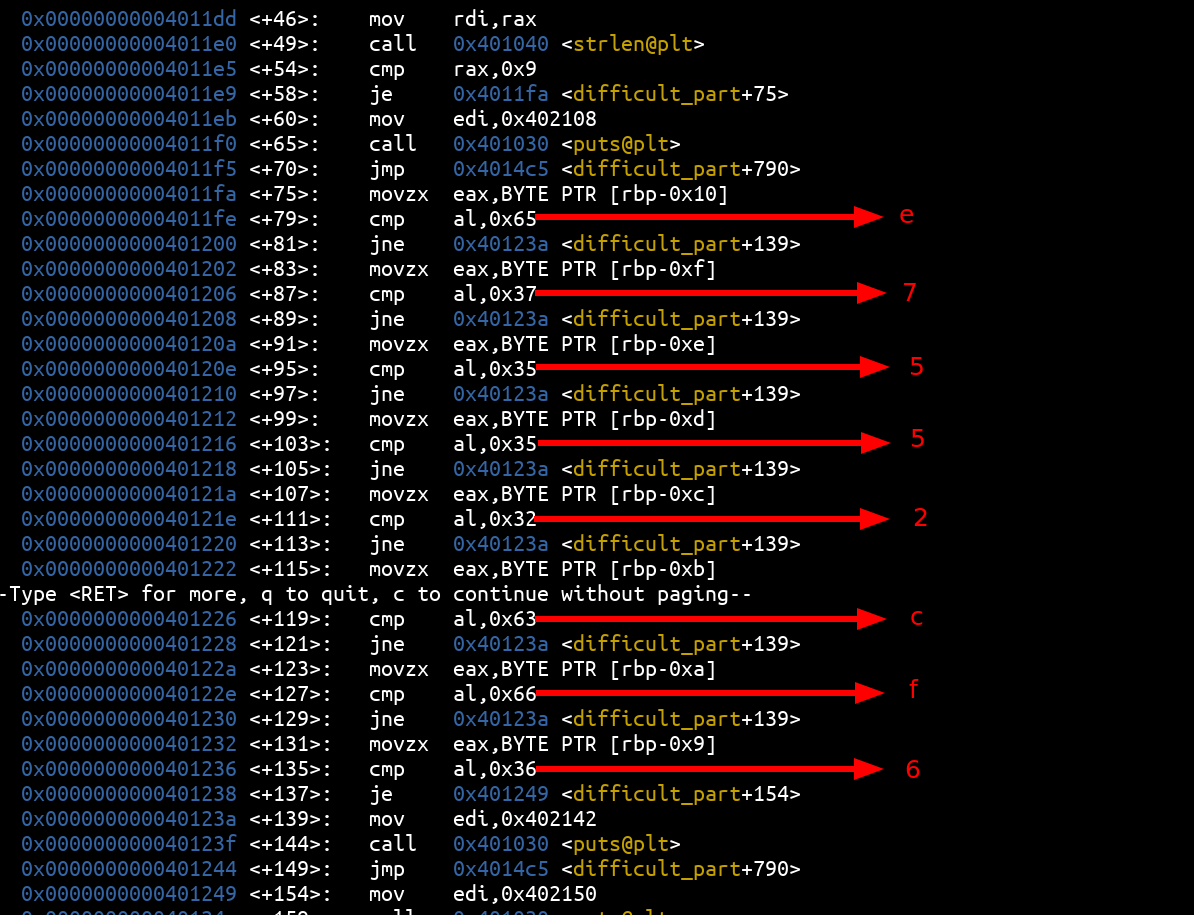
So now we have:
FCSC{e7552cf6________________________}
Part 2
The second check works a little differently and introduces a slight calculation on the compared values:
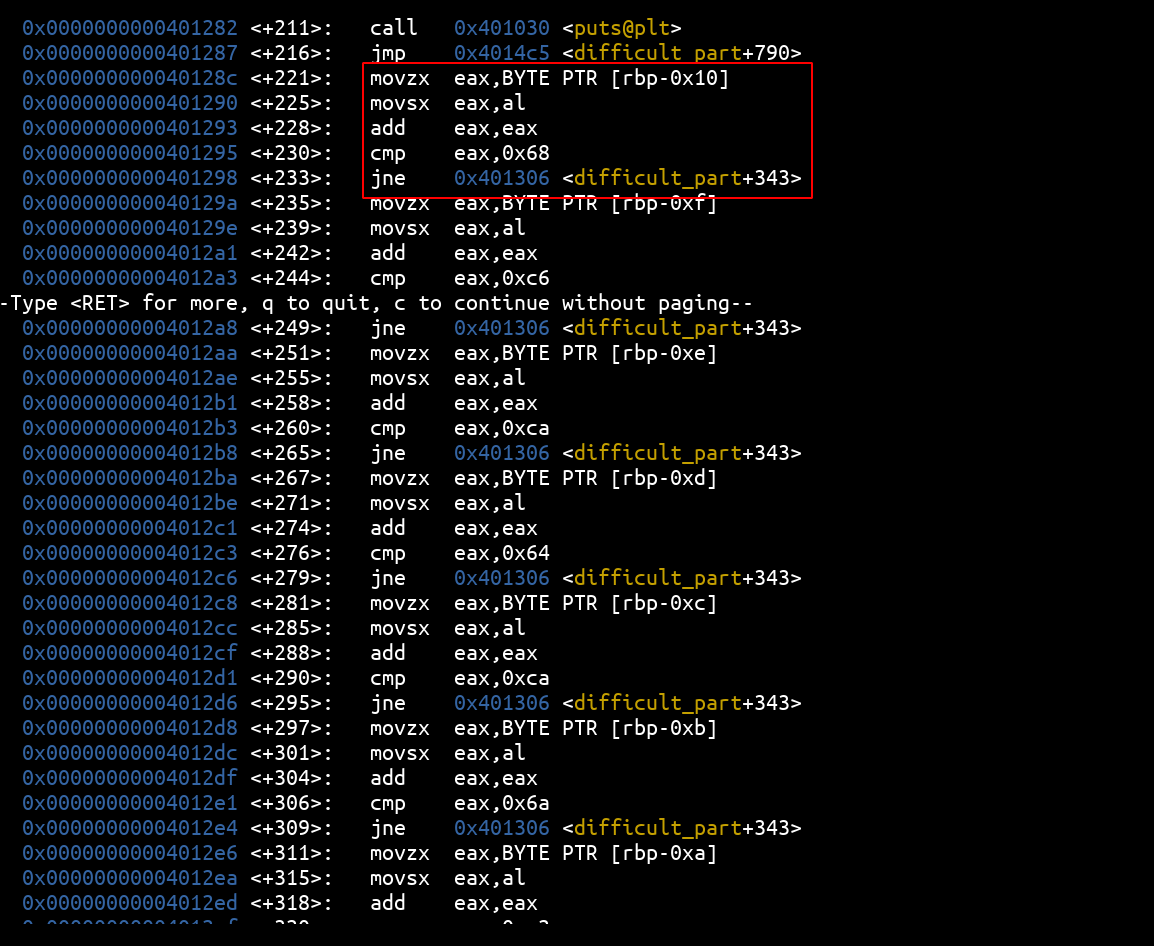
We notice that each block allowing to check a character is composed like this:
0x000000000040128c <+221>: movzx eax,BYTE PTR [rbp-0x10]
0x0000000000401290 <+225>: movsx eax,al
0x0000000000401293 <+228>: add eax,eax
0x0000000000401295 <+230>: cmp eax,0x68
0x0000000000401298 <+233>: jne 0x401306 <difficult_part+343>
The ASCII value of the flag characters we entered is read, then placed in eax. Then this value is multiplied by 2 (add eax, eax is equivalent to eax + = eax in a programming language) before being compared. To reconstruct the expected values, we can do it simply in python:
>>> cmp_values = [0x68,0xc6,0xca,0x64,0xca,0x6a,0xc2,0xc8]
>>> ascii_vals = [c//2 for c in cmp_values]
>>> bytes(ascii_vals)
b'4ce2e5ad'
>>>
So now we have:
FCSC{e7552cf64ce2e5ad________________}
Part 3
In this check, the ASCII value of the flag characters we entered is read, then placed in eax then the shl operation is performed.
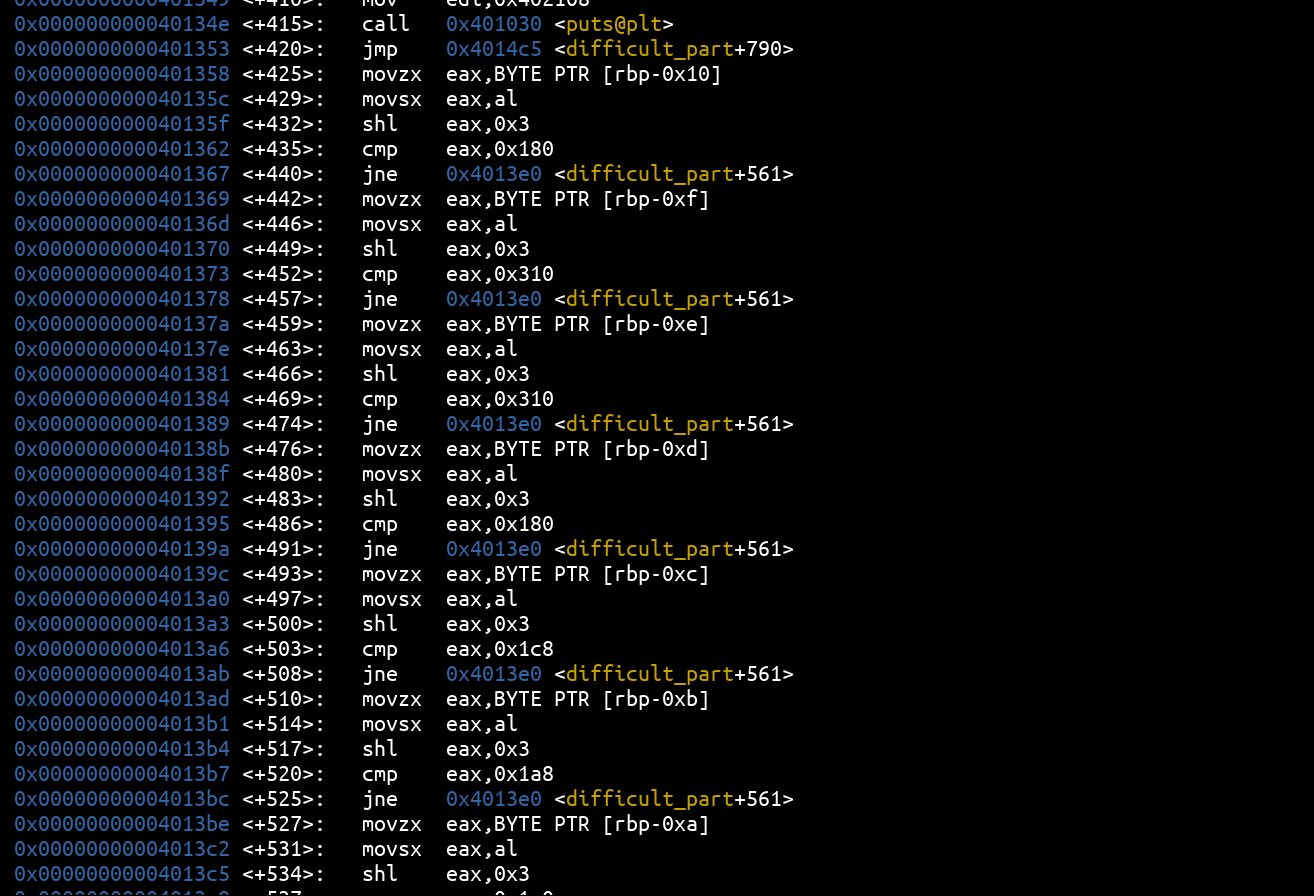
The instruction shl in assembler allows to perform a left shift ( shift left) by a specified number of bits (here shl eax, 0x3 shifts eax by 3 bits to the left, which is equivalent to to a multiplication by 2³).
0x0000000000401358 <+425>: movzx eax,BYTE PTR [rbp-0x10]
0x000000000040135c <+429>: movsx eax,al
0x000000000040135f <+432>: shl eax,0x3
0x0000000000401362 <+435>: cmp eax,0x180
0x0000000000401367 <+440>: jne 0x4013e0 <difficult_part+561>
To find the expected values, we can do it simply in python and performing a division by 8 or a right shift variable >> 3:
>>> cmp_values = [0x180,0x310,0x310,0x180,0x1c8,0x1a8,0x1a0,0x330]
>>> ascii_vals = [c//(2**3) for c in cmp_values]
>>> bytes(ascii_vals)
b'0bb0954f'
>>>
We now have almost the entire flag:
FCSC{e7552cf64ce2e5ad0bb0954f________}
Part 4
The last part carries out an xor of two values in the stack, and compares their result.
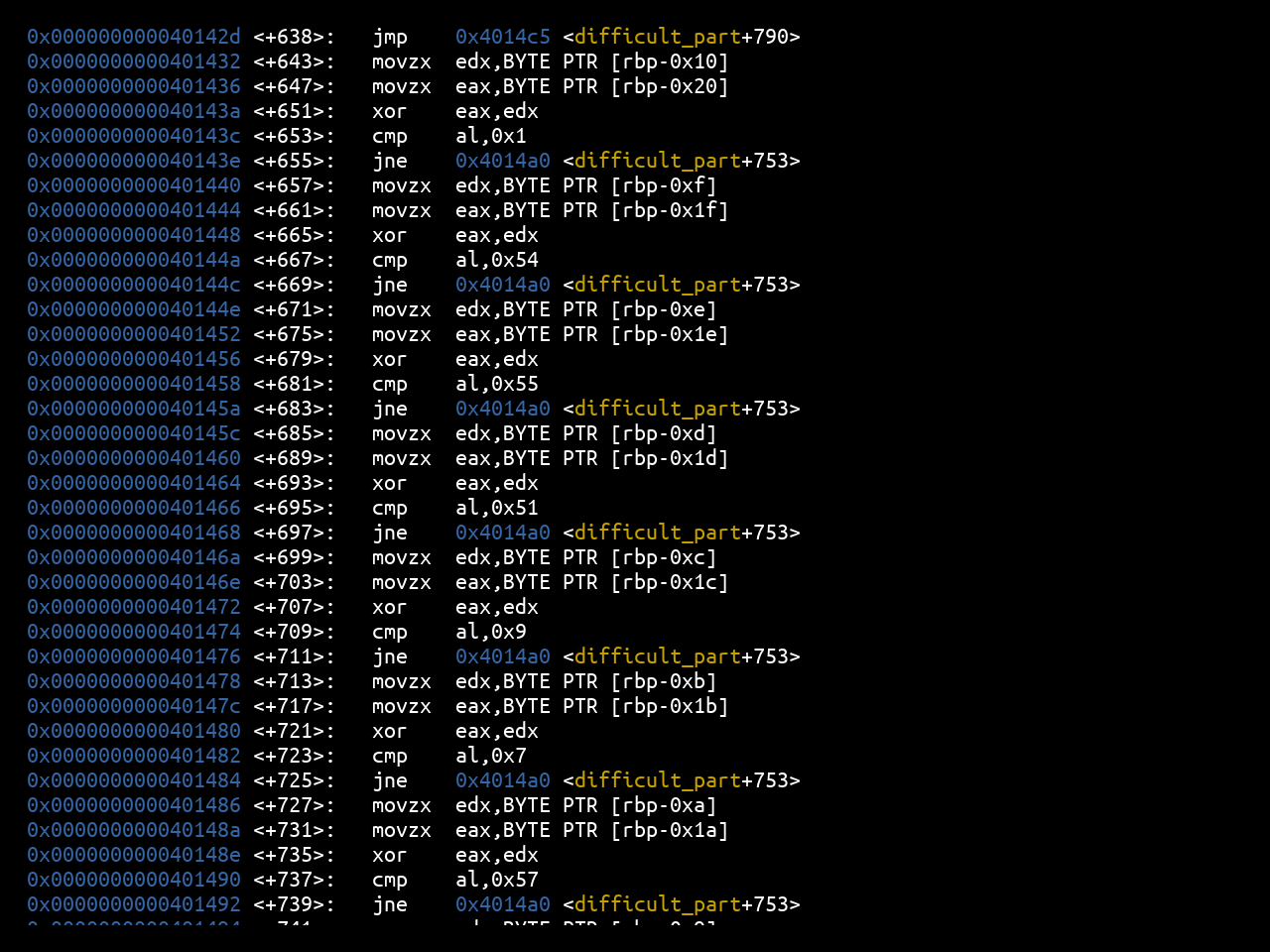
To be able to retrieve these values, just put a breakpoint at the level of the xor:
0x0000000000401432 <+643>: movzx edx,BYTE PTR [rbp-0x10]
0x0000000000401436 <+647>: movzx eax,BYTE PTR [rbp-0x20]
0x000000000040143a <+651>: xor eax,edx
0x000000000040143c <+653>: cmp al,0x1
0x000000000040143e <+655>: jne 0x4014a0 <difficult_part+753>
And repeat it for the 8 checks of the flag characters:
b * 0x000000000040143a
b * 0x0000000000401448
b * 0x0000000000401456
b * 0x0000000000401464
b * 0x0000000000401472
b * 0x0000000000401480
b * 0x000000000040148e
We just have to read each time the value present in edx and perform an xor with the value expected by the comparison, to find the ASCII characters of the flag.
>>> flag_part_4 = [0x30^0x1, 0x62^0x54, 0x62^0x55, 0x30^0x51, 0x39^0x9, 0x35^0x7, 0x34^0x7, 0x66]
>>> bytes(flag_part_4)
b'167a023f'
>>>
We now have the whole flag (without the trailing brace }):
FCSC {e7552cf64ce2e5ad0bb0954f167a023f
But the difficult_part function then calls the most_difficult_part function, which we will analyze right after.
Analysis of the most_difficult_part function
The most_difficult_part is the hardest of all this challenge (just kidding) it’s a very simple function that only checks the last character of the flag (which we can guess, it’s necessarily a} ):
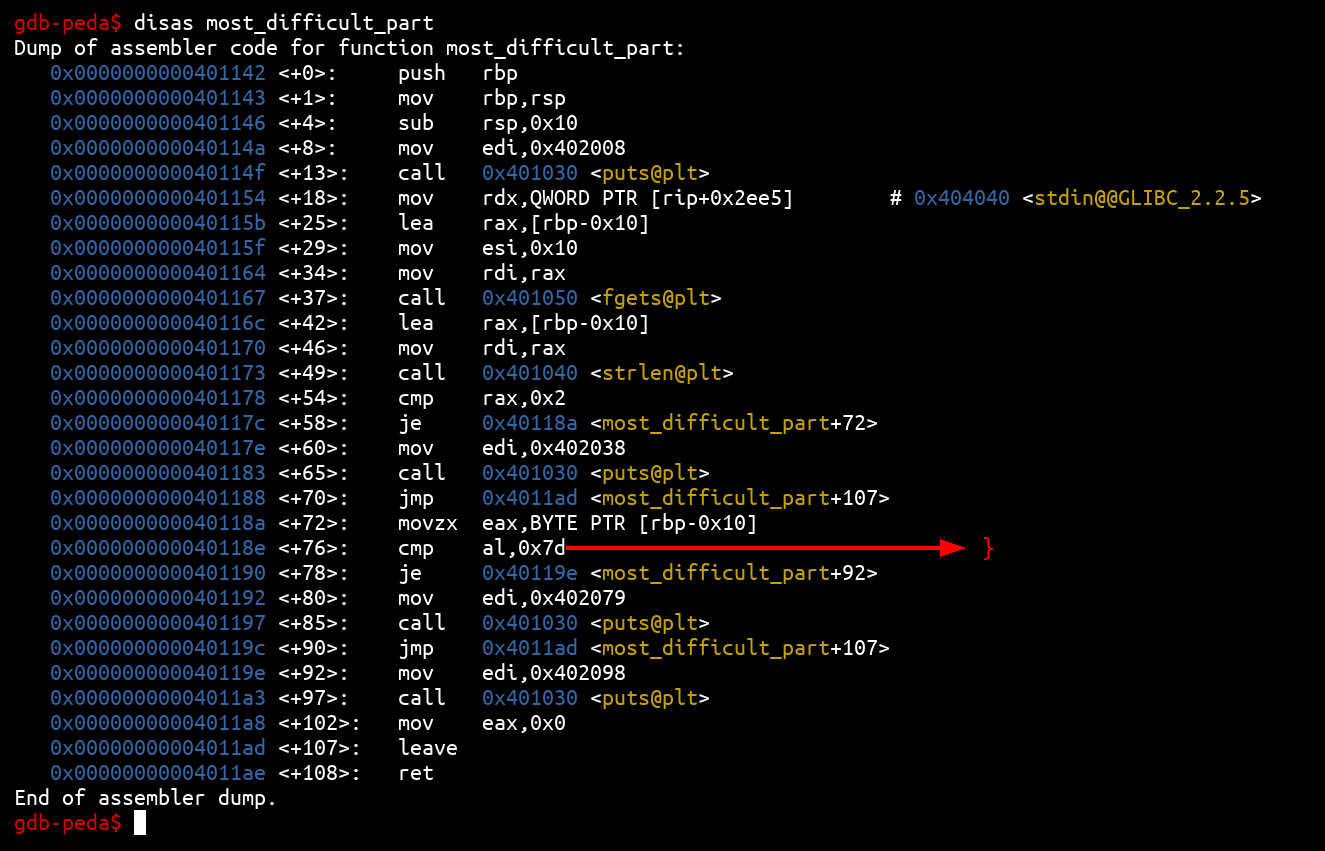
And we have the flag:
FCSC {e7552cf64ce2e5ad0bb0954f167a02cf}